GSAS Profile Terms

Peaks Profile terms for Rietveld Analysis

Most Rietveld refinement programs use a pseudo-Voigt term combining Gaussian and Lorentzian peak shapes (plus other correction terms). In general, the X-ray source can be described by a Gaussian function, while sample effects are described by Lorentzian terms.

For the synchrotron powder XRD data from 11-BM, the instrumental resolution is well described by Gaussian terms. Sample effects, such as size and microstrain broadening (i.e. local variations in the lattice parameters) are usually fit best by Lorentzian terms.

Please consult other references (such as the GSAS manual) for details on Rietveld profile functions.

11-BM Profile Fitting

Representative LaB6 data for 11-BM (high resolution powder XRD) can be downloaded from the 11-BM webpage here (pick your format):

Full details for the dataset collected in Feb. 2010 are as follows:

precise wavelength = 0.412235 A
data was collected on a spinning 0.8 mm diameter capillary of LaB6 660a
The NIST LaB6 660a SRM certificate lattice value = 4.15691(1) A. 
The estimated muR (X-ray absorption) is ~ 1.0 
collection temp: 295 K
2theta range: 0.5 deg - 50.0 deg
step size: 0.001 deg

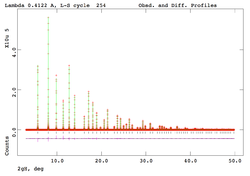
For the 11-BM dataset collected on LaB6 in Feb. 2010, the following parameters provide a good Rietveld fit using GSAS/EXPGUI:

space group: Pm-3m
a =  4.156917(1)
zero shift:  -0.00029 deg 2theta
La   @ 0, 0, 0 (Ui/Ue*100 =  0.62)
B  @  0.1984(1), 1/2, 1/2  (Ui/Ue*100 =  0.29)
 
GSAS Profile type 4:  (non-listed terms = 0.0)
Coeff.   :      GU        GV         GW          LX         S/L     H/L
Value    :  2.552E+00 -5.439E-01  5.990E-02   2.790E-01  1.2E-03  1.2E-03
background = 4-term Shifted Chebyschev (type #1)

Gives the following Rietveld fit statistics

wRp = 6.45%,  Rp = 4.86%,  CHI**2 = 3.349 (for 14 variables)                 

Image of fit plot is shown below (click to enlarge):

Conversion of pseudo-Voigt function terms

GSAS <-> Fullprof Gaussian Parameters GSAS Term <=> Fullprof Term : (description) GU = 1803.4 * U : (instrumental term, ~ tan^2 of theta) GV = 1803.4 * V : (instrumental term, ~ tan of theta) GW = 1803.4 * W : (instrumental term, ~ constant with theta) GP = 1803.4 * IG : (size broadening)

note: 1083.4 => centidegrees squared divided by 8*ln(2)

Lorentzian Parameters GSAS Term <=> Fullprof Term : (description) LX = 100 * Y : (size broadening) LY = 100 * X : (microstrain)

note: 100 => degrees to centidegrees

Finger-Cox-Jephcoat asymmetry parameters GSAS S/L = Fullprof S_L GSAS H/L = Fullprof D_L

Note: terms are equivalent

S / L = the sample “half height”/diffractometer radius H / L = the slit half height/diffractometer radius

"Typical values of Rietveld instrument profile coefficients" Kaduk J, Reid J. Powder Diffraction (2011) vol. 26 pp. 88

size and microstrain broadening (i.e. local variations in the lattice parameters) are Lorentzian for 11-BM data

Only rarely is Gaussian size broadening observed; this re- quires a very tight monodisperse distribution, which is rarely encountered in powder specimens but is sometimes seen in polycrystalline solid specimens such as pieces of metal.

GSAS Refinement Hints

GSAS Profile 4 anisotropy Sxxx terms

Q: What is the "best" order for incorporating profile 4 anisotropy Sxxx terms into a refinement?

A: from Robert Von Dreele (July 28, 2011)
 "Usually, I do the S4xx ones first & then the others. The thing is fairly stable after that.
Do do all of them at once in any case  in the end. The S4xx must be > 0 but the rest can be any sign.
If you want a quick way of seeing the shape, run mustrplot (spelling?) in GSAS; 
you'll need gnuplot to see the plot. For monoclinics, it might look like two beans back-to-back."
-Bob